Each bacterial transformant (plasmid vectors) or in vitro packaged virus particle (phage vectors) represents a single vector molecule joined to a unique foreign DNA fragment.
The population of transformants or virus particles obtained is called a library - and in the primary library, each individual bacterium or virus is unique.

Since our objective in constructing such a library is to identify and isolate a specific foreign DNA fragment, it is important that all DNA sequences in the sample are represented by one or more individual recombinant(s).

We have already looked at the pattern of genomic fragments generated by restriction enzyme digestion of genomic DNA.
If cut with a 4-mer enzyme, the average fragment size is approximately 256 bp.
Similarly, digestion with a 6-mer enzyme generates an average fragment size of approximately 4000 bp
and digestion with an 8-mer generates an average fragment size of 64,000 bp.
For each of these digests, fragments larger and smaller than the average are also produced.

Given the size limitations imposed by the various vector systems,
recombinant plasmids greater than 10 kb transform bacteria very inefficiently,
lambda insertrion vectors cannot package inserts greater than 10 kb in size
lambda subsititution vectors can only accomodate inserts between 10 and 20 kb in size,
complete genomic digests with 6-mer or 8-mer enzymes will produce large genomic DNA fragments which will not be represented in a library using any of these vector systems.

In order to ensure that all genomic sequences are represented in our libraries, we must generate random genomic fragments and make a probability estimate of the probability with which our specific DNA fragment will be included in a statistically relevant number or recombinant molecules.

To generate the random genomic DNA fragments and ligate them into our selected vector , we focus our attention on pairs of enzymes which generate compatable ends to facilitate ligation.
One of these enzymes must cut the genome frequently (ie a 4-mer) so that we can obtain a random population of genomic fragments,
while the other must cut uniquely in the vector (ie a 6-mer enzyme).
The most common enzymes used for this purpose are SauIIIA and BamHI.

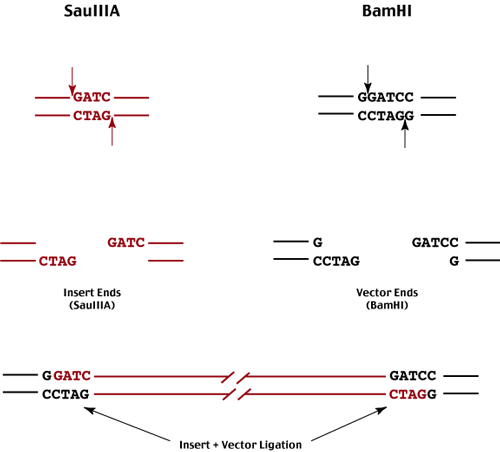
In order to generate a random population of genomic DNA fragments using an enzyme that cuts frequently, we use partial digest conditions where then enzyme only cuts the genome at a fractions of its recognition sites (limit enzyme concentration or time of digest or both).

Following partial digestion of the genomic DNA, we isolate an appropriate size class of genomic fragments - each end of each fragment represents one of many possible SauIIIa sites.

These fragments are then ligated into a BamHI digested vector - either plasmid or lambda insertion or substitution vector.

Each recombinant transformant or packaged phage resulting from this ligation represents an individual random genomic fragment.

This produces a population of recombinant molecules that contain many overlapping genomic fragments - any given genomic sequence will be represented by several of these overlapping fragments.

There are two statistical approaches used to estimate the number of recombinants required.

The first is the 'lazy molecular biologist's rule of thumb':

First, we calculate the number of individual recombinants that contain sufficient genomic DNA sequence to represent one complete genome - the genome equivalent.

To approximate this distribution the 'rule of thumb' stipulates that

For the human genome,

a random shotgun plasmid library constructed using genomic inserts of 6 kb needs to contain at least